Passons du 9x9 au 27x27

Le placement de tous les candidats potentiels permet de résoudre les grilles faciles mais est surtout le passage obligé pour la résolution des grilles plus complexes.

Pour cela il faut passer d'une grille 9x 9 à une grille 27x27 afin d'y placer tous les candidats potentiels et d'avoir une lisibilité la plus aisée possible.

Ce passage nécessite une certaine rigueur.

Pour ma part j'utilise Excel (mais le logiciel gratuit OpenOffice est tout à fait adapté) et comme vous pouvez le constater dans mes solutions proposées dans la rubrique "BLOG COLORIAGE VIRTUEL" j'ai pris les conventions suivantes pour distinguer du statut du candidat (Origine - Potentiel - Validé)

Les candidats de la grille d'origine sont en rouge gras et taille 14

Les candidats potentiels sont en noir normal et taille 10

Les candidats validés (solution de la grille) sont en bleu gras et taille 14

Pour terminer les candidats d'origine et validés sont centrés dans la case

Les candidats potentiels sont placés de la façon suivante

1 en Haut à Gauche - 2 en Haut au Milieu - 3 en Haut à Droite

4 au Centre à Gauche - 5 au Centre au Milieu - 6 au Centre à Droite

7 en Bas à Gauche  - 8  en Bas au Milieu - 9 en Bas à Droite

Pour chaque case vide et pour chaque candidat il faut analysé les 3 zones sudokus (Ligne - Colonne - Bloc)

Exemple Si la case L1C1 est vide on place le candidat 1 que si le 1 est absent des 3 zones sudoku L1 - C1 -B1

A contrario si le 1 est présent dans une des 3 zones sudoku L1 - C1 - B1 il ne peut être présent en L1C1

Rien de mieux qu'un exemple pour la compréhension du passage de la grille 9x9 à 27x27 et le placement des candidats potentiels

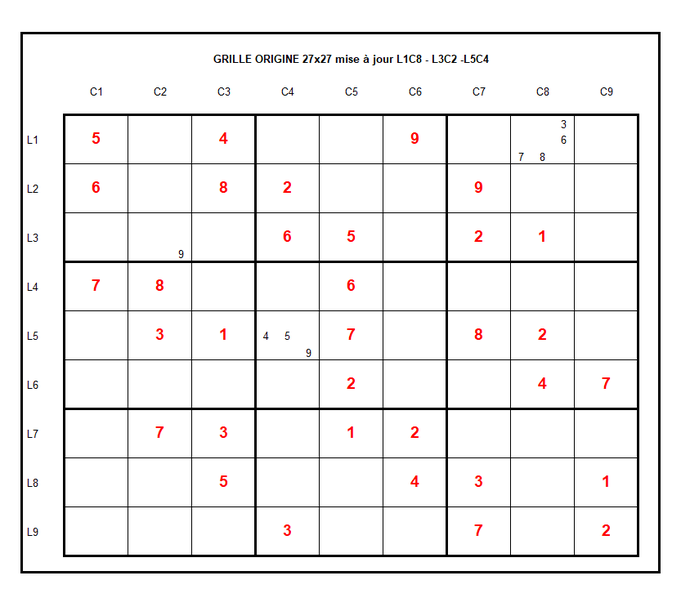
Passons en revue 3 cases : L1C8 - L3C2 - L5C4

Pour L1C8 analysons L1 - C8 - B3

1 n'est pas candidat potentiel car présent en C8 & B3

2 n'est pas candidat potentiel car présent en C8 & B3

3 est candidat potentiel car absent de L1 & C8 & B3

4 n'est pas candidat potentiel car présent en L1 & C8

5 n'est pas candidat potentiel car présent en L1

6 est candidat potentiel car absent de L1 & C8 & B3

7 est candidat potentiel car absent de L1 & C8 & B3

8 est candidat potentiel car absent de L1 & C8 & B3

9 n'est pas candidat potentiel car présent en L1 & B3

Quatre candidats potentiels en L1C8 : 3 - 6 - 7 - 8

Pour L3C2 analysons L3 - C2 - B1

1 n'est pas candidat potentiel car présent en L3

2 n'est pas candidat potentiel car présent en L3

3 n'est pas candidat potentiel car présent en C2

4 n'est pas candidat potentiel car présent en B1

5 n'est pas candidat potentiel car présent en L3 & B1

6 n'est pas candidat potentiel car présent en L3 & B1

7 n'est pas candidat potentiel car présent en C2

8 n'est pas candidat potentiel car présent en C2 & B1

9 est candidat potentiel car absent de L3 & C2 & B1

Un candidat potentiel en L3C2 : 9

Pour L5C4 analysons L5 - C4 - B5

1 n'est pas candidat potentiel car présent en L5

2 n'est pas candidat potentiel car présent en L5 & C4 & B5

3 n'est pas candidat potentiel car présent en L5 &C4

4 est candidat potentiel car absent de L5 & C4 & B5

5 est candidat potentiel car absent de L5 & C4 & B5

6 n'est pas candidat potentiel car présent en C4 & B5

7 n'est pas candidat potentiel car présent en L5 & B5

8 n'est pas candidat potentiel car présent en L5

9 est candidat potentiel car absent de L5 & C4 & B5

Trois candidats potentiels en L5C4 : 4 - 5 - 9

Complétons la grille de tous les candidats potentiels

ET SI ON CONTINUAIT .......